세제곱근 계산기

세제곱근 계산기는 양수의 세제곱근(3제곱근)을 구해야 하는 모든 이에게 꼭 필요한 도구입니다. 이 다재다능한 도구는 세제곱근을 찾는 과정을 단순화할 뿐 아니라 숫자 세제곱 연산도 손쉽게 수행할 수 있게 해줍니다. 수학 문제 해결, 완전 세제곱수 판별, 또는 다른 차수의 근 계산 등 어떤 목적이든 세제곱근 계산기가 정확성과 효율을 보장합니다.
숫자의 세제곱근이란?
어떤 숫자의 세제곱근이란 그 수를 세 번 곱했을 때 원래의 숫자가 되는 값을 말합니다. 수식으로는 ³√x = y이며, 이는 y³ = x를 의미합니다.
또는 ³√x = x^(1/3)로 표현할 수도 있습니다.
예를 들어 27의 세제곱근을 구하라고 하면 y³ = 27을 만족하는 숫자를 찾는 것입니다. 그 답은 3인데, 3 × 3 × 3 = 27이기 때문입니다. 이 개념은 산수, 대수학 및 더욱 고급 수학 분야에서 기본이 됩니다.
세제곱근의 기하학적 이해
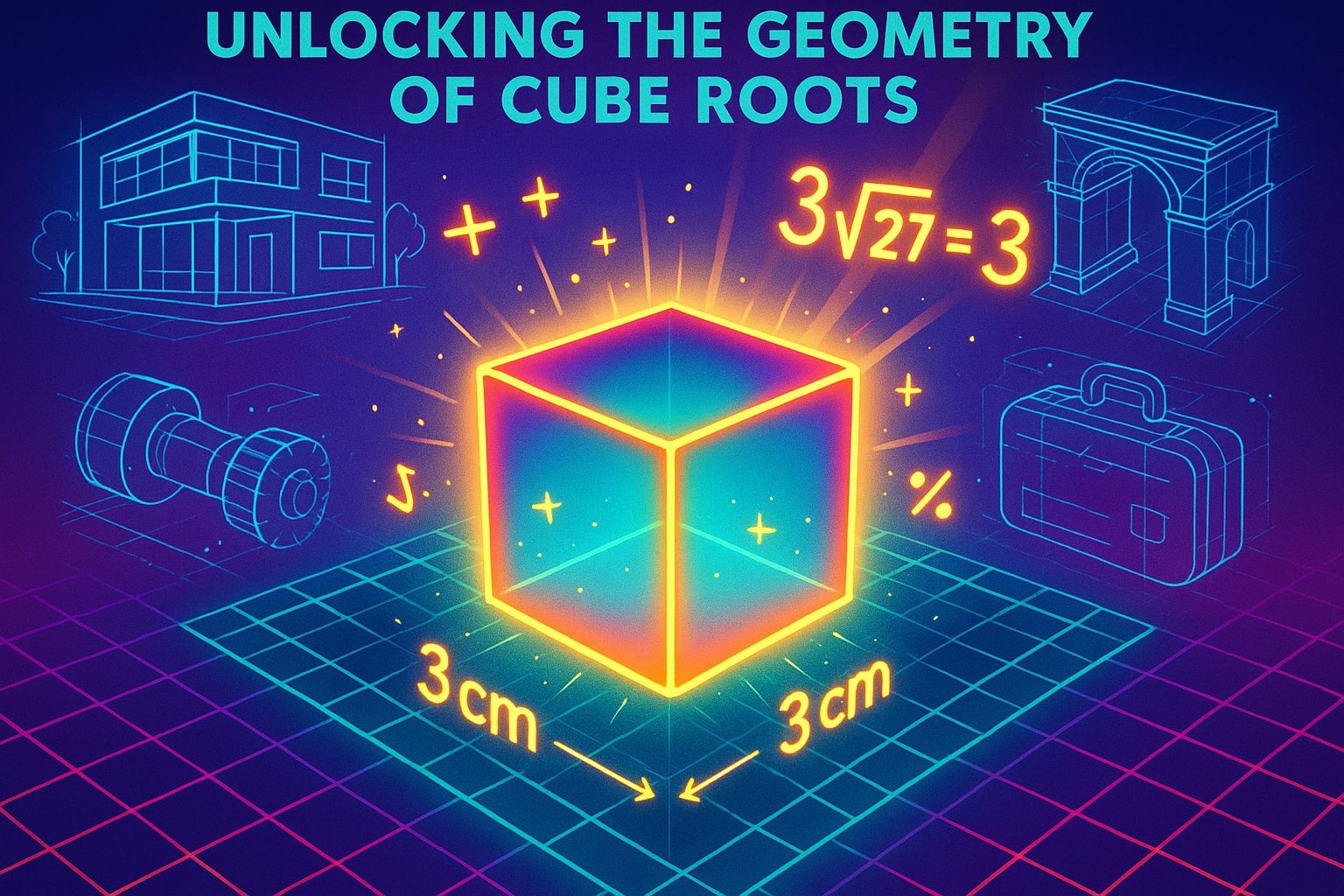
세제곱근에는 공간적 해석도 있습니다. 부피가 27㎤인 정육면체를 생각해 보세요. 한 변의 길이를 알기 위해서는 27의 세제곱근을 계산해야 합니다. 그 결과 3cm가 되는데, 이는 3³ = 27이기 때문입니다.
이런 실용적 연결 덕분에 세제곱근은 기하학, 공학, 건축학, 제품 설계 등 3차원 공간 이해가 중요한 분야에서 매우 유용합니다.
2차원 설계 관련 계산은 정사각형 면적 계산기를 참고하세요.
완전 세제곱수란?
완전 세제곱수는 정수를 세제곱하여 얻은 수를 말합니다. 이 값을 알고 있으면 문제 해결이 훨씬 빨라집니다. 자주 쓰이는 예시는 다음과 같습니다.
이 값들은 기하학, 물리학, 수학에서 빠른 참조와 계산에 자주 활용됩니다. 주어진 수가 정수의 세제곱으로 표현될 수 있는지 판단하거나 세제곱근 계산 시 유용합니다.
| 수 | 완전 세제곱수 |
|---|---|
| 1³ | 1 |
| 2³ | 8 |
| 3³ | 27 |
| 4³ | 64 |
| 5³ | 125 |
| 6³ | 216 |
| 7³ | 343 |
| 8³ | 512 |
| 9³ | 729 |
| 10³ | 1,000 |
세제곱근 함수와 그래프
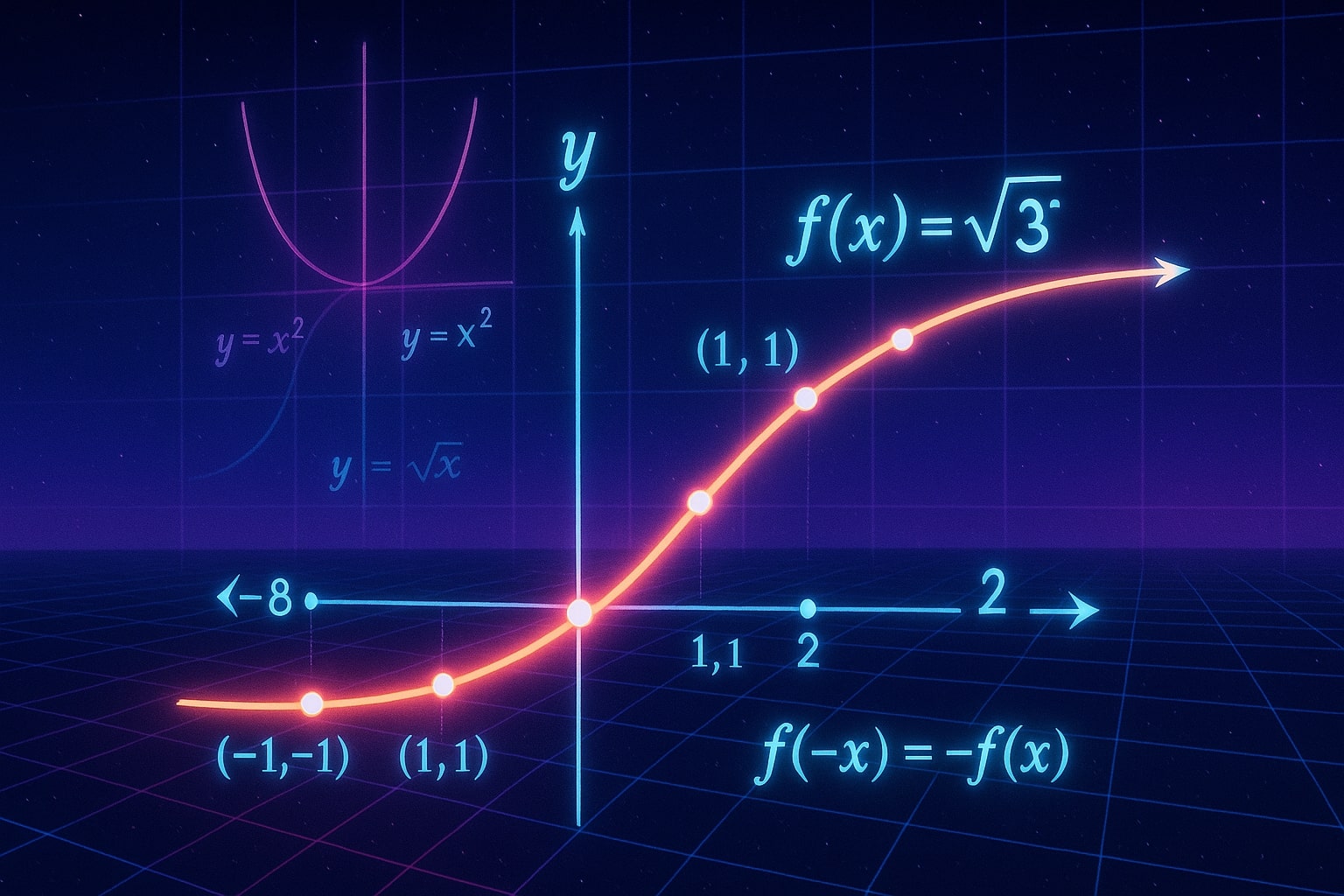
세제곱근 함수는 f(x) = ³√x로 쓰이며, 원점을 기준으로 회전 대칭을 가지는 기함수입니다. 이 성질은 다음과 같이 표현됩니다.
f(−x) = −f(x)
세제곱근 함수의 특징:
- 원점을 지난다: (0, 0)을 그래프가 통과합니다.
- 정의역·치역: 모두 실수 전체(ℝ)입니다.
- 거동: x가 양의 무한대로 갈 때 y도 증가하고, x가 음의 무한대로 갈 때 y는 감소합니다.
³√x = y 그래프는 완만한 곡선을 그리며, 제곱근 함수나 이차 함수의 그래프처럼 급격하게 변하지 않아 시각적으로 구별됩니다.
2차 함수와 비교해 보고 싶다면 제곱근 계산기를 이용해 보세요.
이 외에 다양한 도구는 수학 계산기 전체 모음을 확인하세요.
