곡선형 정원 배치부터 원형 극장 설계에 이르기까지, 부채꼴 면적은 원형 공간을 계획할 때 핵심 개념입니다. 이 가이드는 원의 기초 기하학을 이해하고 다양한 실제 활용 사례를 살펴보며 흥미로운 사실도 전해드립니다.
다른 도형에 대해서도 알아보고 싶으신가요? 제곱피트 면적 계산기 모음을 확인해 보세요.
부채꼴 면적이란?
부채꼴은 피자 조각, 파이 차트의 한 구간 또는 원형 화단의 일부처럼 원의 한 조각을 의미합니다. 이는 두 반지름과 그 사이의 호로 정의됩니다. 부채꼴 면적은 그 조각의 넓이를 말하며, 일반적으로 제곱피트 단위로 측정합니다.
전체 원은 360도이므로, 부채꼴의 크기는 원의 반지름과 조각의 각도에 따라 달라집니다. 예를 들어, 90° 부채꼴은 원 전체의 4분의 1에 해당합니다.
이 개념은 원형 분수대 배치, 레이더 범위 지도, 무대 위 스포트라이트가 비추는 면적 계산 등 다양한 분야에서 활용됩니다.
💡 흥미로운 사실: NASA는 인공위성의 신호 커버리지를 계획할 때 부채꼴 면적 공식을 사용합니다. 많은 위성이 원형 또는 방사형 패턴으로 신호를 전송하기 때문에, 부채꼴 면적 계산을 통해 위성 배치를 최적화하고 통신 구역 중복을 방지합니다.
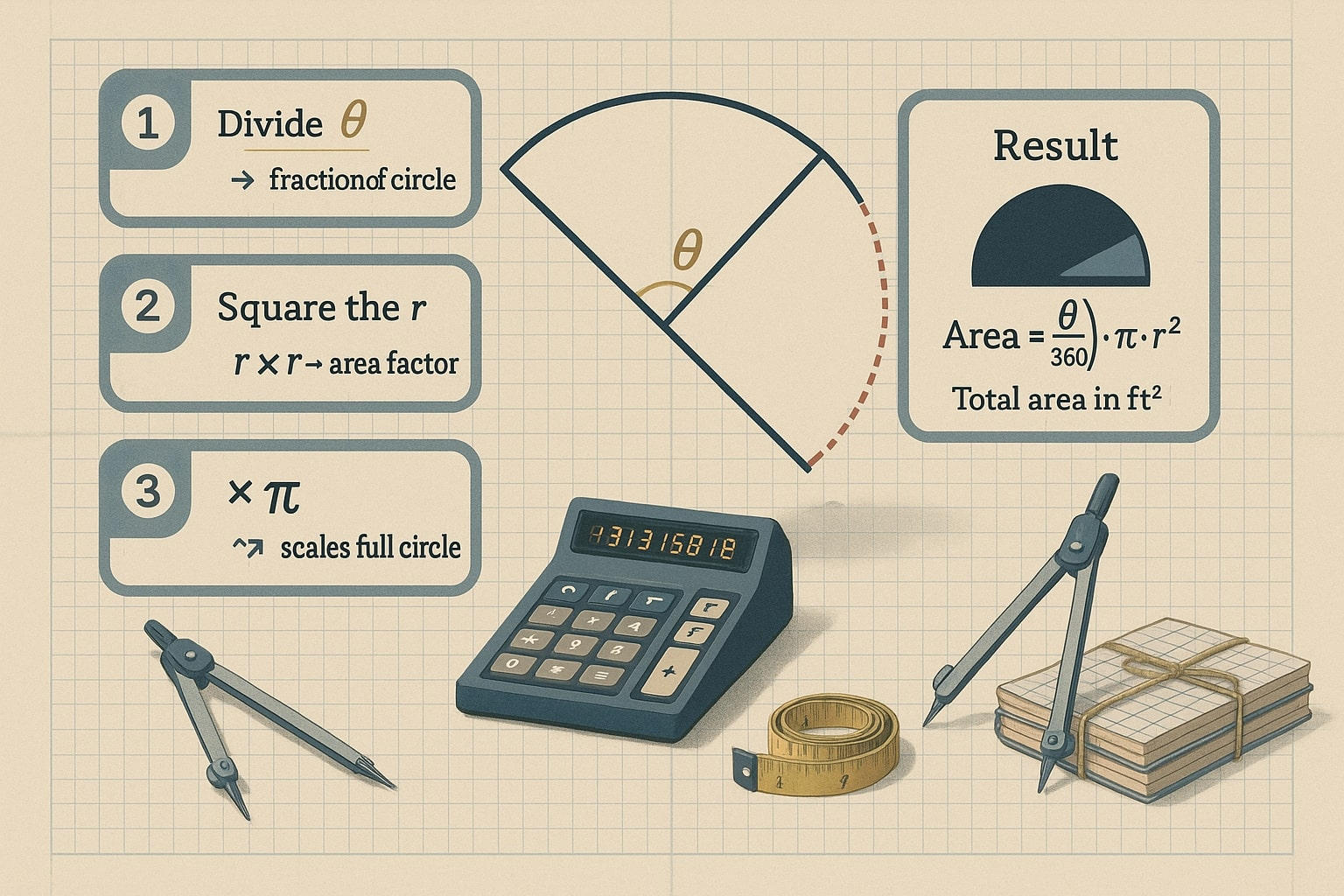
부채꼴 면적 계산 방법 (예제 포함)
부채꼴 면적을 구하는 방법은 간단한 공식 하나로 해결됩니다:
부채꼴 면적 = (θ / 360) × π × r²
각 항목을 살펴보면:
-
θ는 부채꼴의 중심각(도 단위)입니다.
-
r는 원의 반지름(중심에서 가장자리까지의 거리)입니다.
-
π는 상수로, 약 3.1416입니다.
공식은 전체 원에서 차지하는 비율을 계산합니다. 전체 원은 360도이므로, 각도를 360으로 나누면 부채꼴이 차지하는 비율이 나옵니다.
예제: 반지름이 6ft인 원형 화단에서 120° 부채꼴의 면적을 구해 보겠습니다.
1단계: 값 확인
-
반지름 (r) = 6ft
-
각도 (θ) = 120°
2단계: 공식 적용면적 = (120 / 360) × π × (6²)= (1/3) × π × 36= π × 12≈ 3.1416 × 12≈ 37.7 제곱피트
따라서 이 부채꼴의 면적은 약 37.7제곱피트입니다.
부채꼴, 직사각형 등 여러 형태를 결합한 복잡한 도형은 제곱피트 면적 계산기를 활용해 세부적으로 나누어 계산하면 보다 정확한 전체 면적을 구할 수 있습니다.

교토의 원 정원
일본 교토의 한적한 선사 뒤에 자리한 이 정원은 현지인들에게 ‘円の庭(엔 노 니와)’ 또는 ‘원들의 정원’으로 불립니다. 처음 보면 잔잔한 물결처럼 돌과 이끼, 자갈이 방사형으로 배치된 미니멀한 공간이라 생각할 수 있지만, 그 속에는 수백 년 전의 원형 기하학이 깊이 녹아 있습니다.
이 정원은 선불교의 원을 상징하는 엔소에서 영감을 받았습니다. 1600년대 후반에 개조된 기록에 따르면, 승려들은 숙련된 정원사들과 함께 손으로 그린 부채꼴 도면을 사용해 호의 너비를 계산했고, 완벽한 균형과 시각적 조화를 유지하도록 설계했습니다.
비록 당시에는 ‘부채꼴 면적’이라는 용어를 사용하지 않았지만, 그 개념은 같았습니다. 각도와 반지름을 측정해 이끼와 자갈이 정확한 면적을 차지하도록 배치함으로써, 사찰의 명상 플랫폼 한 지점에서 바라볼 때 가장 아름다운 리드미컬한 흐름을 완성했습니다.
수학 문제를 빠르고 쉽게 풀고 싶다면 수학 섹션을 확인해 보세요.


