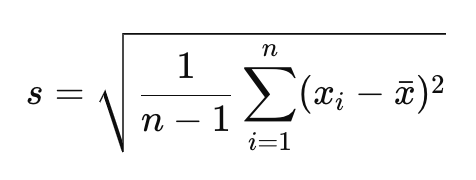표준편차 계산기

표준편차는 학교에서 수학 수업이나 연구 보고서 어딘가에서 들어봤을 개념일 겁니다. 다소 낯선 이름 뒤에는 과학 연구부터 비즈니스 전략, 기상 예보까지 다양한 분야에서 핵심 역할을 하는 직관적인 아이디어가 숨어 있습니다. 간단히 말해, 평균값을 기준으로 값들이 얼마나 퍼져 있는지를 나타내는 지표입니다. 변동성을 측정하면 일상적으로 다루는 데이터에 대한 명확한 이해와 확신을 얻을 수 있습니다.

더 많은 계산기를 보려면 수학을 확인하세요.

표준편차란 무엇인가?

표준편차는 데이터 집합의 값들이 평균으로부터 얼마나 떨어져 있는지를 측정합니다. 다시 말해 “값들이 평균에서 얼마나 벗어나는가?”를 수치로 보여주는 도구입니다.

예를 들어, 한 반의 모든 학생이 100점 만점에 정확히 80점을 받았다고 합시다. 평균은 80이고, 모든 점수가 동일하므로 표준편차는 0입니다. 즉, 변동이 전혀 없습니다. 반면에 또 다른 반의 평균도 80점이지만 학생들의 점수가 60, 70, 90, 100점이었다고 하면 평균은 같아도 점수 분포가 훨씬 넓어지고 표준편차도 커집니다.

표준편차가 낮으면 데이터가 평균 근처에 밀집해 있다는 의미이고, 높으면 값들이 더 넓게 퍼져 있다는 뜻입니다.

왜 데이터의 변동성이 중요할까?

변동성은 단순한 통계적 잡음이 아닙니다. 표준편차로 데이터의 등락 폭을 파악하면 추세나 이상치, 숨겨진 패턴을 발견할 수 있습니다. 의료 분야에선 치료 효과의 일관성을 평가하고, 기후 과학에선 온도 변화를 추적하며, 교육 분야에선 학교별 학생 성취도를 분석합니다. 공학에서는 품질 관리를 위해 필수적으로 사용하죠. 변동성을 모르면 데이터가 실제로 무엇을 말하는지 오해할 수 있습니다.

관련 도구를 사용해 보세요: 평균 계산기, 분산 계산기, Z-점수 계산기 등으로 데이터의 이야기를 더 깊이 탐구해 보세요.

모집단 표준편차

연구 대상 전체의 데이터를 보유하고 있을 때는 모집단 표준편차를 계산할 수 있습니다. 이 방법은 전체 데이터의 정확한 변동 정도를 파악하는 데 사용됩니다. 예를 들어, 모집단의 모든 개인이나 조사 대상 전체의 데이터를 알고 있을 경우 적용합니다.

모집단 표준편차 공식:

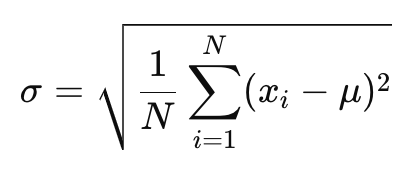
여기서:

σ: 모집단 표준편차,

N: 관측값 개수(모집단 크기),

x_i: 데이터 내 각 값,

μ: 모집단 평균.

표본 표준편차

모집단 전체가 아닌 표본 데이터만 있을 때는 표본 표준편차를 사용해 모집단 표준편차를 추정합니다. 표본 표준편차는 편향을 보정하기 위한 ‘자유도’ 보정을 포함해 변동성을 과소평가하지 않도록 설계되었습니다.

표본 표준편차 공식:

여기서:

s: 표본 표준편차,

n: 표본 관측값 개수,

x̄: 표본 평균.

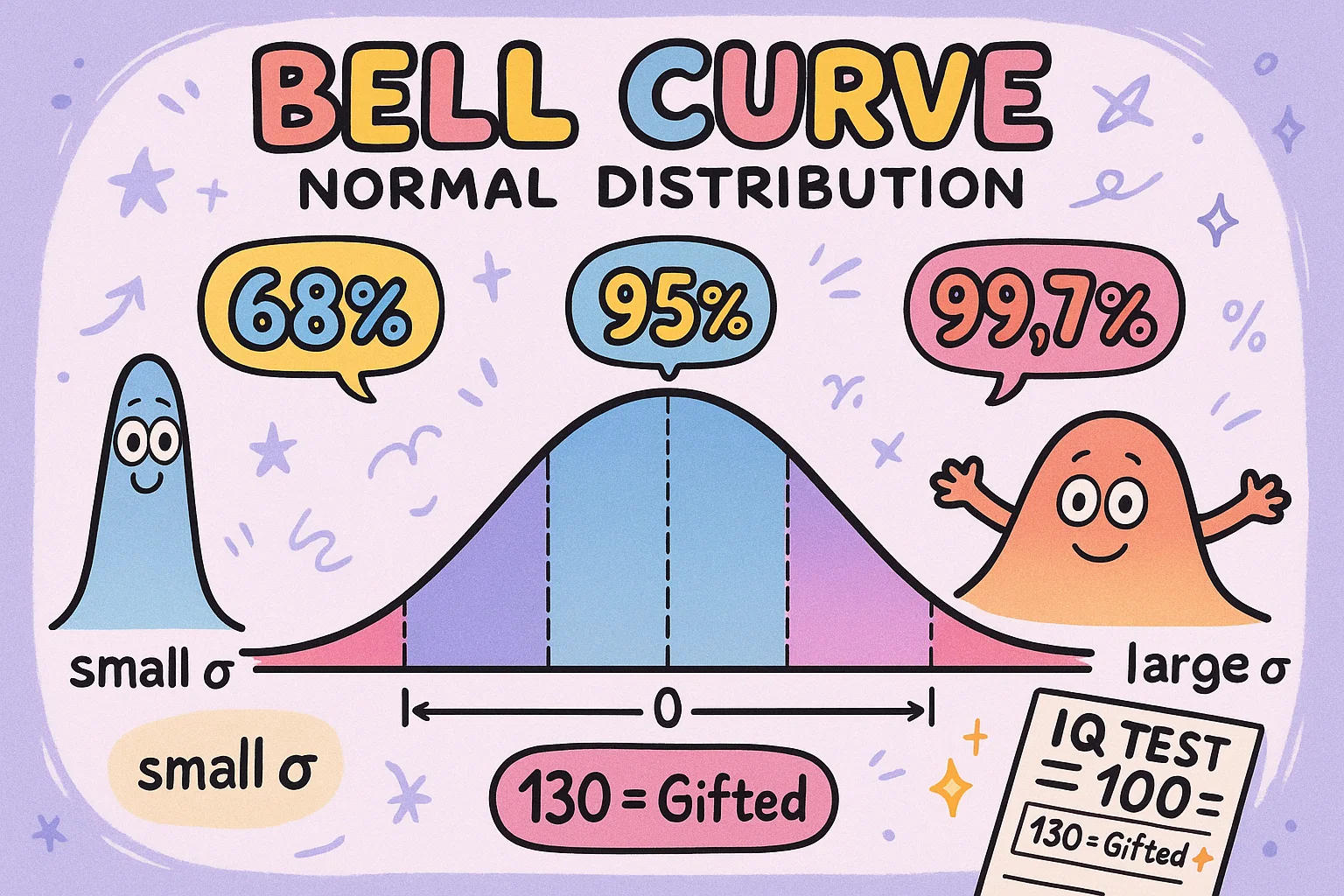
벨 곡선과 정규분포

벨 곡선(종 모양 그래프)은 대부분의 값이 중앙에 몰리고 극단값은 적게 분포하는 정규분포를 시각화한 것입니다. 이 곡선은 키, IQ 점수, 시험 성적, 혈압 수치 등 현실에서 자주 나타납니다.

표준편차는 이 곡선의 폭을 결정합니다. 값들이 평균에 가까이 몰려 있으면 곡선이 좁고 높아지며(작은 표준편차), 분산이 크면 곡선이 넓고 낮아집니다(큰 표준편차).

다음 규칙을 기억하세요:

• 68%의 값이 평균에서 1표준편차 이내에 있음

• 95%가 2표준편차 이내

• 99.7%가 3표준편차 이내

이 규칙을 통해 특정 값이 얼마나 일반적인지, 또는 드문지를 빠르게 판단할 수 있습니다.

🎯 재미 팁: 대부분의 IQ 테스트는 평균 100, 표준편차 15로 설계돼 있습니다. 그래서 IQ 130은 상위권으로 간주됩니다!