솔직히 말해 "타원체(ellipsoid)"라는 단어는 일상 대화에서 자주 쓰이지 않습니다. 하지만 놀랍게도 타원체는 우리 주변에 아주 많습니다. 계란을 품어본 적 있나요? 럭비공을 던져본 적 있나요? 우주에서 본 지구를 떠올려보세요. 모두 타원체의 예입니다. 원뿔부터 피라미드까지 다양한 3D 도형의 부피는 메인 부피 계산기 페이지에서 찾아보실 수 있습니다.
타원체란 정확히 무엇일까요?
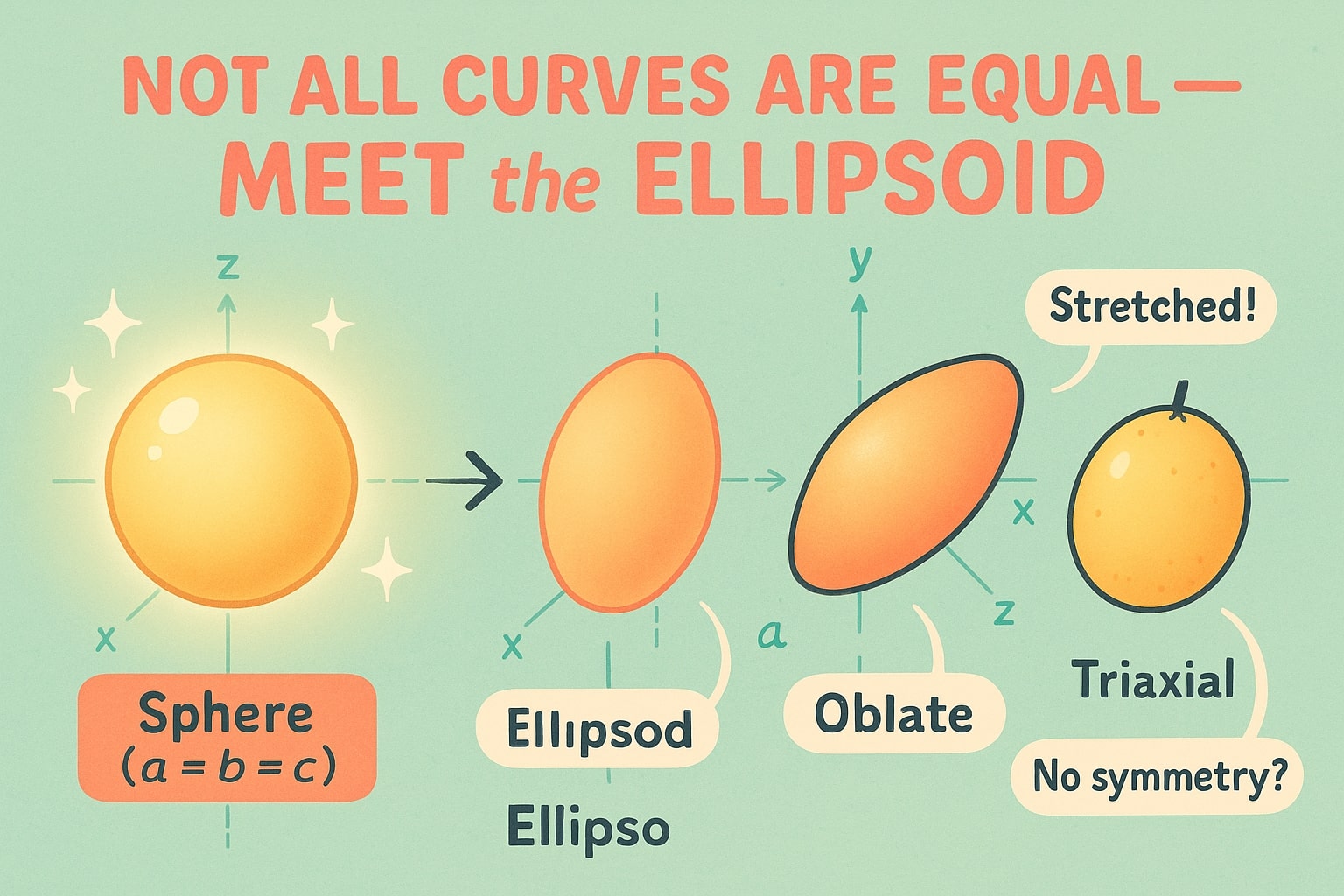
먼저 완벽한 3D 구형인 구(sphere)를 떠올려보세요. 이제 이를 살짝 눌러 납작하게 만들거나 옆으로 늘려 보세요. 모든 방향이 같지 않은 매끄러운 둥근 형태가 바로 타원체입니다.
기하학적으로 타원체는 세 개의 축으로 표현됩니다:
a = x축 방향의 길이
b = y축 방향의 길이
c = z축 방향의 길이
만약 a, b, c가 모두 같다면 축하합니다—그것은 구입니다. 다르면, 타원체 영역에 있는 것입니다.
일반적인 유형은 다음과 같습니다:
길게 늘어난 타원체(prolate ellipsoids): 한 축을 따라 늘어난 형태(예: 럭비공)
납작한 타원체(oblate ellipsoids): 한 축을 따라 납작한 형태(예: 지구)
삼축 타원체(triaxial ellipsoids): 세 축 모두 다른 길이로 대칭이 없으며, 특이한 모양의 과일이나 약 캡슐과 비슷합니다.
행성, 세포, 어류의 알 등 다양한 곳에서 타원체를 접할 수 있습니다. 그래서 그 부피를 계산하는 방법을 아는 것이 매우 유용합니다.
부피를 계산한 뒤에는 부피 변환기를 통해 리터, 갤런 등 다른 단위로 쉽게 변환할 수 있습니다.
타원체 부피 계산법
좋은 소식입니다: 부피 공식은 매우 간단합니다. 세 개의 반축(semiaxis) 길이(a, b, c)만 알면 다음 공식에 대입하면 됩니다:
부피 = (4/3) × π × a × b × c
이렇게 세 반축을 곱하고 파이(π)를 곱한 뒤, 4/3을 곱하면 부피가 나옵니다.
빠른 팁: 꼭 반축 길이를 사용하세요, 전체 지름이 아닙니다. 예를 들어 타원체 너비가 10cm라면 반축 길이는 5cm를 써야 합니다.
예를 들어, 반축이 각각 4cm, 3cm, 2cm라면
부피는 이렇게 계산합니다:
부피 = (4/3) × π × 4 × 3 × 2 = (4/3) × π × 24 ≈ 100.53 cm³
만약 세 반축 모두 같아 5cm라면, 이 타원체는 사실 구와 같으므로 공식도 고전적인 구 공식으로 단순해집니다:
부피 = (4/3) × π × r³
💡 전문가 팁: 형태가 거의 구형이라면 구 공식으로도 부피를 추정할 수 있고, 저희 구 부피 계산기를 활용하면 편리합니다.
가우스와 지구의 형태
19세기 초, 위성이나 구글 어스가 없던 시절, 독일의 수학자 칼 프리드리히 가우스(Carl Friedrich Gauss)는 대담하게 질문했습니다. 지구의 실제 모양은 무엇인가?

대부분 사람들은 지구가 완벽한 구형이라고 생각했지만, 가우스는 의심했습니다. 지구가 극지방에서 약간 납작하다는 가설, 즉 오늘날 우리가 납작한 타원체(oblate ellipsoid)라고 부르는 형태입니다. 이론에만 그치지 않고 그는 직접 산을 오르고 장비를 들고 다니며 정확한 거리 측정 기법을 개발했습니다.
그의 선구적인 연구는 지구형 및 크기를 연구하는 과학인 측지학(geodesy)의 기반을 다졌으며, 실제로 지구는 완벽한 둥근 구가 아니며, 적도에서 부풀어오르고 극지방에서 납작해지는 사실이 밝혀졌습니다. 이는 위성 시스템 설계나 전 세계 좌표 계산에 큰 영향을 미칩니다.
타원체에 관한 흥미로운 사실
- 지구는 완벽한 구가 아닙니다. 실제로는 납작한 타원체로, 적도 부분이 더 넓습니다. 이 차이는 밀리미터 단위지만, GPS와 우주 항해에 매우 중요합니다.
- 계란은 자연스러운 거의 타원체 형태입니다. 완벽하지는 않지만 닭알은 타원체와 매우 흡사해, 농업 연구에서 부피 추정에 타원체 공식이 활용됩니다.
- 많은 우주 암석과 위성은 타원체 모양입니다. 그 이유는 중력이 충분히 강해 완벽한 구로 모양을 만들지 못하기 때문입니다.
- 의료 영상에서도 타원체가 활용됩니다. MRI와 초음파 기술은 전체 3D 스캔 없이도 기관들의 부피를 타원체 근사로 추정해 효율적으로 측정합니다.
학생, 교육자, 전문가를 위해 디자인된 수학 도구 라이브러리에는 이 외에도 수십 가지 유용한 계산기가 준비되어 있습니다.

