직각삼각형 계산기

직각삼각형이란?

직각삼각형은 한 각이 정확히 90°인 삼각형을 말합니다. 이 하나의 직각은 '다리'라고 불리는 두 변이 해당 모서리에서 만나고, 그 직각의 마주편에 더 긴 변인 '빗변'이 만들어집니다. 대체로 다리는 a와 b로, 빗변은 c로 표기합니다.

직각삼각형은 지붕 경사부터 다리 지지대, 거리등의 그림자에 이르기까지 우리 주변 어디에서나 쉽게 찾아볼 수 있습니다. 수학에서는 몇 개의 숫자만으로 미지의 변이나 각도를 구할 수 있기 때문에 특히 선호됩니다.

직각삼각형이 특별한 이유는 세 변 사이에 내재된 관계성에 있습니다. 피타고라스 정리에 따라 두 변만 알면 항상 세 번째 변을 구할 수 있습니다. 이 때문에 직각삼각형은 기초 기하학부터 삼각법, 물리학의 기본이 됩니다.

직각삼각형 계산 방법

모든 직각삼각형은 하나의 간단한 규칙을 따릅니다: a² + b² = c²

이는 피타고라스 정리이며, 두 다리(a와 b)와 빗변(c)을 연결합니다. 이 중 두 변만 알면 나머지 변을 항상 구할 수 있습니다.

예를 들어 다리의 길이가 각각 3과 4라면, 빗변은:

c = √(3² + 4²) = √(9 + 16) = 5

이 3–4–5 삼각형은 숫자가 깔끔해 고전적 예시로 자주 사용되지만, 같은 규칙은 소수점이나 큰 값의 직각삼각형에도 모두 적용됩니다.

빗변과 한 다리를 알 때 누락된 다리 변을 찾는 공식도 있습니다:

• a = √(c² − b²)

• b = √(c² − a²)

이 빠른 공식은 손으로 계산하거나 계산 결과를 다시 확인할 때 간단히 사용할 수 있습니다.

직각삼각형의 각도 구하기

한 변의 길이를 알면 약간의 삼각법을 이용해 각도를 쉽게 구할 수 있습니다. 가장 흔히 쓰이는 방법은 삼각형의 기본 비율을 활용하는 것입니다:

• 탄젠트를 사용: θ = arctan(a⁄b) — 두 다리를 안 경우에 적합합니다.

• 사인을 사용: θ = arcsin(a⁄c) — 다리와 빗변을 알 때 유용합니다.

이 함수들을 사용하면 빠르게 부족한 각도를 구할 수 있습니다. 한 예각을 구하면 다른 예각은 90° − θ로 바로 구할 수 있습니다.

더 정확한 확인이나 추가 학습을 원한다면 삼각법 계산기 같은 도구를 이용해 각도 구하기를 빠르게 수행할 수 있습니다.

직각삼각형의 둘레와 면적

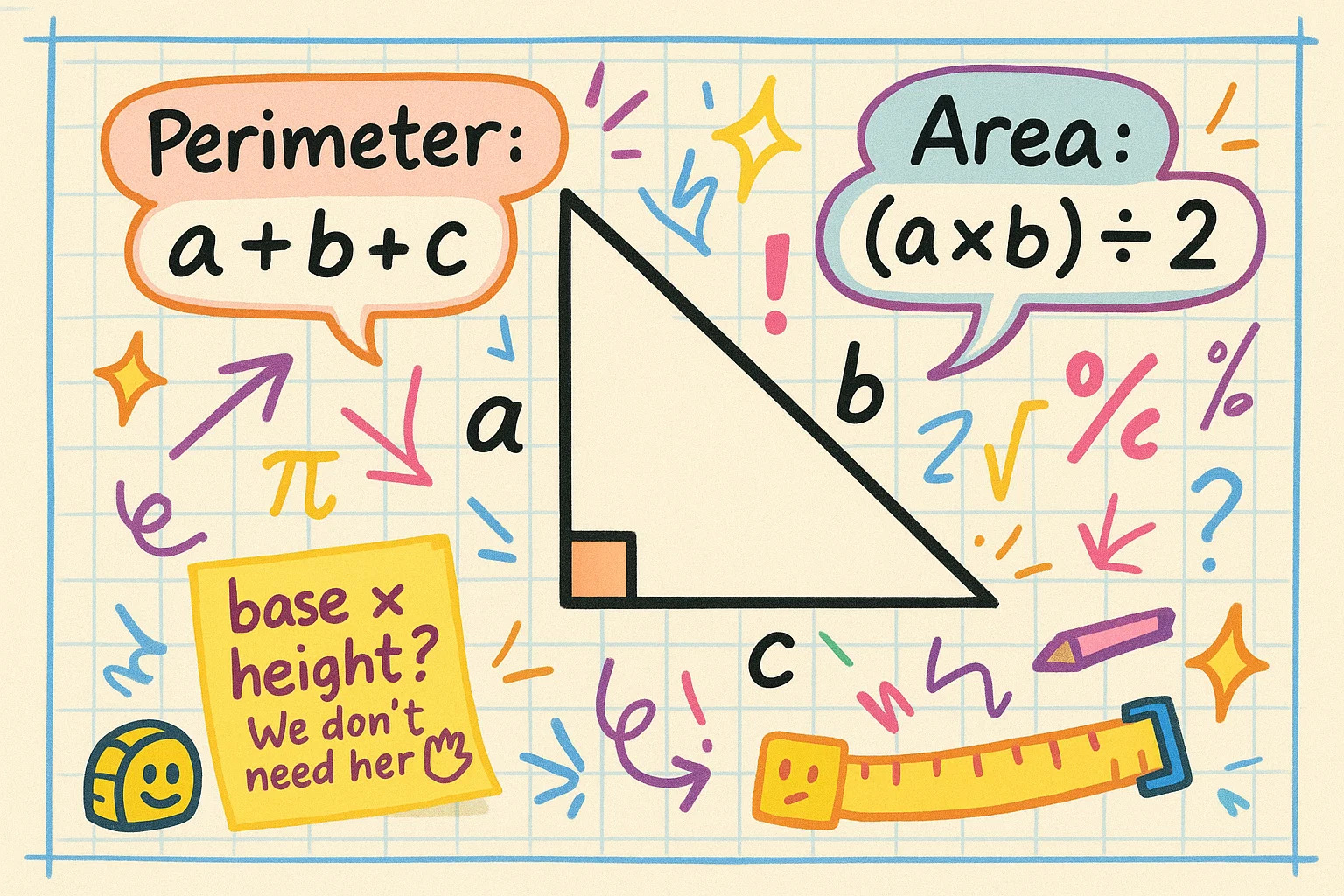
변의 길이를 알면 직각삼각형의 둘레와 면적 계산은 간단합니다. 둘레는 세 변의 합입니다: P = a + b + c

면적은 모든 직각삼각형에 적용되는 공식이 있습니다: A = (a × b) ÷ 2

두 다리가 직각을 이루므로 각각 밑변과 높이 역할을 하기 때문에 별도의 높이선이나 추가 공식이 필요하지 않습니다.

예를 들어 다리 길이가 6과 8인 경우, 빗변 c는 피타고라스 정리로 10입니다. 둘레는 6 + 8 + 10 = 24이고, 면적은 (6 × 8) ÷ 2 = 24입니다.

이 공식들은 숙제나 건설 계획, DIY 프로젝트 설계 등에서 삼각형을 빠르게 파악하는 데 유용합니다.

자주 등장하는 직각삼각형 비율

수학이나 실제 생활에서 자주 쓰이는 직각삼각형은 외워두면 계산을 건너뛰거나 미지의 변과 각을 거의 즉시 구하는 데 도움이 됩니다.

가장 대표적인 두 가지는 다음과 같습니다:

1. 30°–60°–90° 삼각형

• 변의 비율은 항상 1 : √3 : 2입니다.

• 가장 짧은 변(30° 맞은편)을 기준으로, 빗변은 이 값의 2배, 긴 다리는 √3을 곱한 값입니다.

• 두 다리 길이가 같고, 빗변은 다리 길이에 √2를 곱한 값입니다.

• 비율은 1 : 1 : √2입니다.

빠른 참조표:

이 패턴을 알면 기하학이나 삼각법 문제에서 시간을 절약할 수 있습니다.

더 많은 삼각형 문제를 연습하고 싶다면 수학 계산기, 피타고라스 정리 계산기, 그리고 삼각법 계산기를 이용해 보세요.