분수는 레시피, 건축, 세금, 피자 나눔 등 생활 곳곳에 등장합니다. 분수 계산을 잘하면 시간을 절약하고 실수를 줄이며, 학생과 전문가 모두 자신감을 얻을 수 있죠. ⅔ + ¼를 더하는 것부터 ⅝ × ¾를 곱하는 것까지, 이 가이드는 계산 과정을 단계별로 설명하고 자주 헷갈리는 부분을 정리하며, 분수가 실제 문제에 어떻게 적용되는지 보여줍니다.
분수란?
분수는 전체 중 일부를 나타내는 방법입니다. 숫자 두 개를 가로선 위아래로 써서 표현하며, 윗숫자는 분자(가진 부분), 아랫숫자는 분모(전체 단위)를 의미합니다.
피자를 예로 들어 보세요. 피자를 8등분했는데 그중 3조각을 먹었다면, 3⁄8을 먹은 셈입니다. 3은 먹은 조각, 8은 전체 피자를 뜻하죠.
분수는 수학 수업뿐 아니라 일상에서도 자주 쓰입니다. 레시피에는 설탕 ½컵이나 소금 ¾티스푼이 필요하고, 건축·측량에서는 두께가 5⁄8인치인 판자처럼 항상 활용됩니다. 친구들과 식비를 나누거나 할인율을 계산할 때도 분수가 등장하죠.
일상 속 예시:
-
파이의 절반:
½ -
가스 탱크의 3/4:
¾ -
자 눈금의 5/8인치:
5⁄8
분수는 숫자를 유연하게 만들어 짝수로 나누기 어려운 양을 표현할 때 유용합니다.
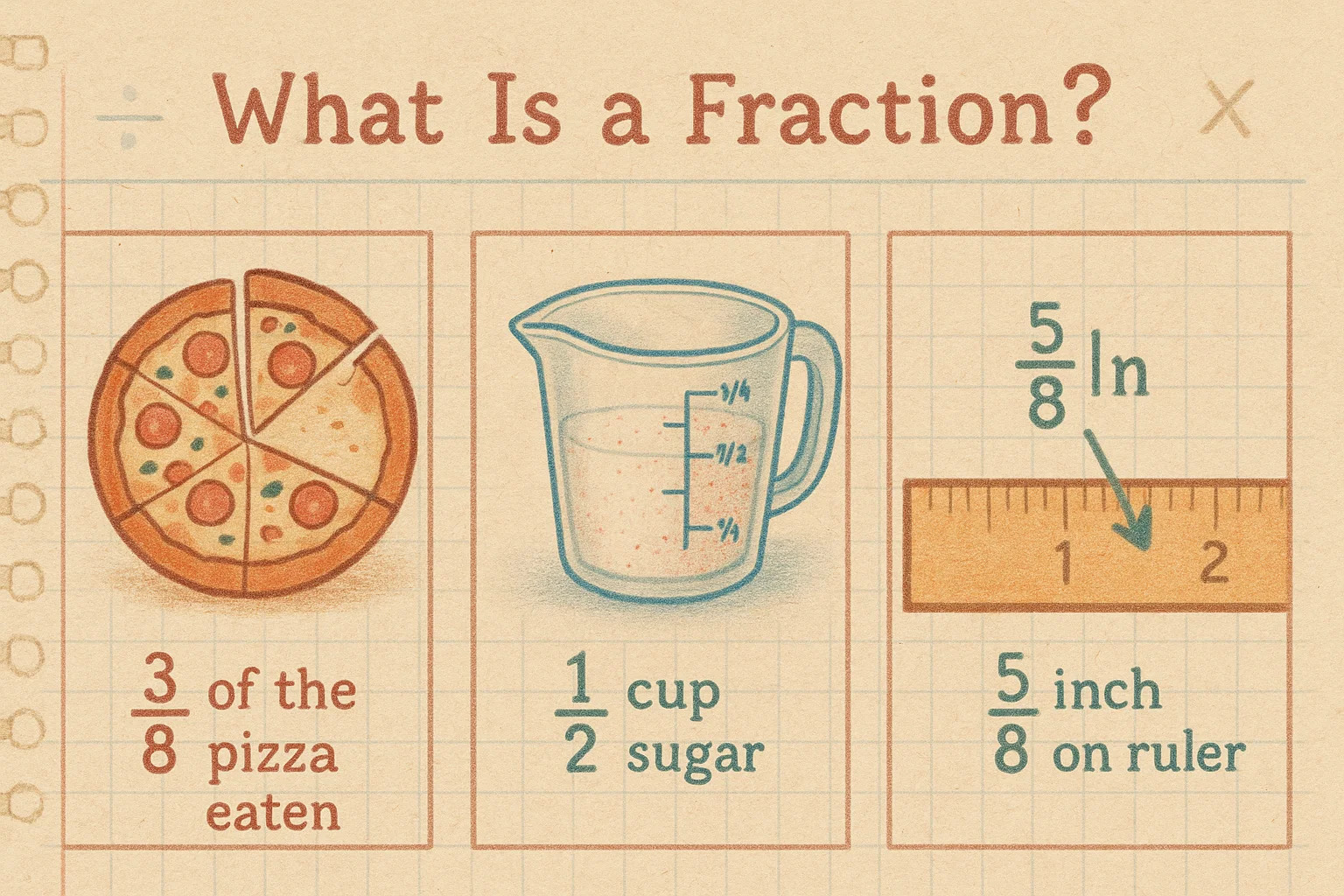
분수 더하기
분모가 같으면 분자를 더하고 분모는 그대로 두기만 하면 되니 분수 더하기는 쉽습니다.
예: 1⁄4 + 2⁄4 = 3⁄4
분모가 다를 땐 공통 분모를 만들어야 합니다. 일반적으로 두 분모의 최소공배수를 공통 분모로 삼고, 분수 값을 그 분모 기준으로 맞춘 뒤 더하면 됩니다.
분모가 다른 예시: 1⁄3 + 1⁄6
-
공통 분모(최소공배수)는 6입니다.
-
1⁄3을2⁄6으로 고칩니다. -
이제
2⁄6 + 1⁄6 = 3⁄6을 계산합니다. -
분자와 분모를 3으로 나누어
3⁄6 = ½로 약분합니다.
간단한 요령: 하나의 분모가 다른 분모의 배수일 때(예: 2와 4), 굳이 최소공배수를 찾지 않고 큰 쪽 분모로 계산해도 됩니다.
분수 빼기
분수 빼기도 더하기와 거의 동일한데, 기호만 마이너스로 바꾸면 됩니다.
분모가 같으면 분자끼리 빼고 분모는 그대로 둡니다.
5⁄8 − 3⁄8 = 2⁄8, 간단히 약분하면 1⁄4입니다.
분모가 다르면 공통 분모를 찾아 분수 값을 맞춘 뒤 분자를 빼면 됩니다.
분모가 다른 예시:5⁄6 − 1⁄3
-
공통 분모는 6입니다.
-
1⁄3을2⁄6으로 고칩니다. -
이제
5⁄6 − 2⁄6 = 3⁄6이므로 -
간단히 약분해
3⁄6 = ½가 됩니다.
조정 후 작은 분수의 분자가 더 크면 결과가 음수가 될 수 있습니다. 예:1⁄4 − 3⁄4 = −2⁄4 = −½.
참고: 결과를 대분수로 바꿀 수도 있지만, 부정 분수(예: −5⁄4) 형태로 남겨도 대부분의 수학 문제에서는 문제가 없습니다.
분수 곱하기
분수 곱셈은 가장 간단한 연산 중 하나입니다. 공통 분모가 필요 없고, 분자끼리 곱하고 분모끼리 곱한 다음 약분하면 끝납니다.
과정별 예시:
예: 2⁄3 × 3⁄5
-
분자 곱하기:
2 × 3 = 6. -
분모 곱하기:
3 × 5 = 15. -
결과:
6⁄15. -
3으로 약분:
6⁄15 = 2⁄5.
정·부정 분수 모두 같은 방법으로 계산합니다.
다른 예시: 5⁄8 × 4⁄10
-
분자:
5 × 4 = 20. -
분모:
8 × 10 = 80. -
결과:
20⁄80. -
20으로 약분해
1⁄4를 얻습니다.
곱하기 전에 교차 약분을 하면 계산이 더 수월합니다. 예: 6⁄10 × 5⁄9
-
곱하기 전 10과 5에 공약수가 있는지 확인합니다.
-
5⁄10을1⁄2로 약분합니다. -
이제
6⁄2 × 1⁄9 = 3 × 1⁄9 = 3⁄9 = 1⁄3가 됩니다.
참고: 1보다 작은 분수로 곱하면 결과도 작아집니다. 예: ¾ × ½ = ⅜
분수 나누기
분수 나눗셈은 처음엔 어려워 보여도, 곱셈에 한 단계만 추가하면 됩니다. 두 번째 분수를 뒤집어(역수) 곱해 주면 되죠.
이 "뒤집어 곱하기" 규칙은 분수 나눗셈을 곱셈으로 바꾸므로 빠르고 실수를 줄여 줍니다.
예: ¾ ÷ ½
-
첫 번째 분수는 그대로 둡니다: ¾.
-
두 번째 분수를 뒤집어
²⁄₁로 만듭니다. -
곱하기:
¾ × ²⁄₁ = ⁶⁄₄. -
2로 약분해
³⁄₂를 얻습니다. -
원하면 대분수 1½로 바꿔도 됩니다.
다른 예시: ⁵⁄₆ ÷ ¹⁰⁄₉
-
¹⁰⁄₉를⁹⁄₁₀로 뒤집습니다. -
곱하기:
⁵⁄₆ × ⁹⁄₁₀ = ⁴⁵⁄₆₀. -
15로 약분해
¾를 얻습니다.
참고: 1보다 작은 분수로 나누면 결과가 커지고, 1보다 큰 분수로 나누면 결과가 작아집니다.
실생활 적용: 레시피에서 ¾컵이 필요한데 반만 만들고 싶다면 ¾ ÷ 2를 계산하게 됩니다. 즉 ¾ × ½ = 3⁄8컵이죠.
기억할 점: 분수 나눗셈에 공통 분모는 필요 없습니다. 항상 두 번째 분수를 뒤집어 곱하세요. 더 빠르고 실수도 줄일 수 있습니다.
분수 연산과 더 큰 수학 개념의 연결
분수는 학교에서 배운 또 다른 개념 같지만, 실제로는 일상과 고급 수학 곳곳에 숨어 있습니다. 분수를 더하고 빼고 곱하고 나누는 모든 과정이 실제 생활과 연관된 아이디어를 담고 있죠.
생각해 보세요:
-
비율과 레시피:
⁸⁄₁₂를²⁄₃로 약분하면 단순화뿐 아니라 비율을 표현합니다. 이 비율로 쿠키 반죽을 두 배로 늘리거나 반만 만들 때도 편리하죠. -
대수학의 기초:
x ÷ ¾ = 2를 풀 때도¾를⁴⁄₃로 뒤집어 곱하는 같은 원리를 씁니다. 방정식 뒤에 숨은 힘은 바로 분수입니다. -
실제 사용하는 단위 변환: 화씨와 섭씨 변환 공식에는
⁵⁄₉라는 분수가 들어갑니다. 시속 마일을 초당 미터로 바꿀 때도 분수가 필수입니다. -
확률과 통계: 주사위를 굴려 4가 나올 확률은
¹⁄₆입니다. 두 사건이 동시에 일어날 확률을 구할 때도 분수 덧셈·곱셈이 활용됩니다.
분수는 가운데에 선이 그어진 숫자 그 이상입니다. 사물의 관계, 비율, 변화를 설명하는 도구이자, 한번 익히면 자연스럽게 활용할 수 있는 바로 그 비밀병기입니다.
재미있는 사실: 고대 이집트인들은 분자의 숫자를 항상 1로만 표현했습니다. 예를 들어
²⁄₃를 쓰려면½ + ¹⁄₆처럼 나눠 적었죠. 현대 분수가 훨씬 편리합니다.