분수 혼합수 계산기

혼합수 — 예를 들어 2 ½ 또는 5 ¾ —는 단순한 학교 수학 문제 이상입니다. 요리법 작성, 목재 판매, 스포츠 거리 측정 방식에 사용됩니다.

혼합수 vs. 가분수

만약 2 ½ 컵의 밀가루를 계량했거나 누군가가 5 ¾ 마일을 달렸다고 들었다면 이미 혼합수를 활용해본 것입니다. 혼합수는 정수와 진분수(분자가 분모보다 작은 분수)를 결합한 형태인 예를 들어 3 ½는 실제로 정수 3과 ½이라는 의미입니다. 매우 실용적이고 친숙하며 일상생활에서 훨씬 자주 사용됩니다.

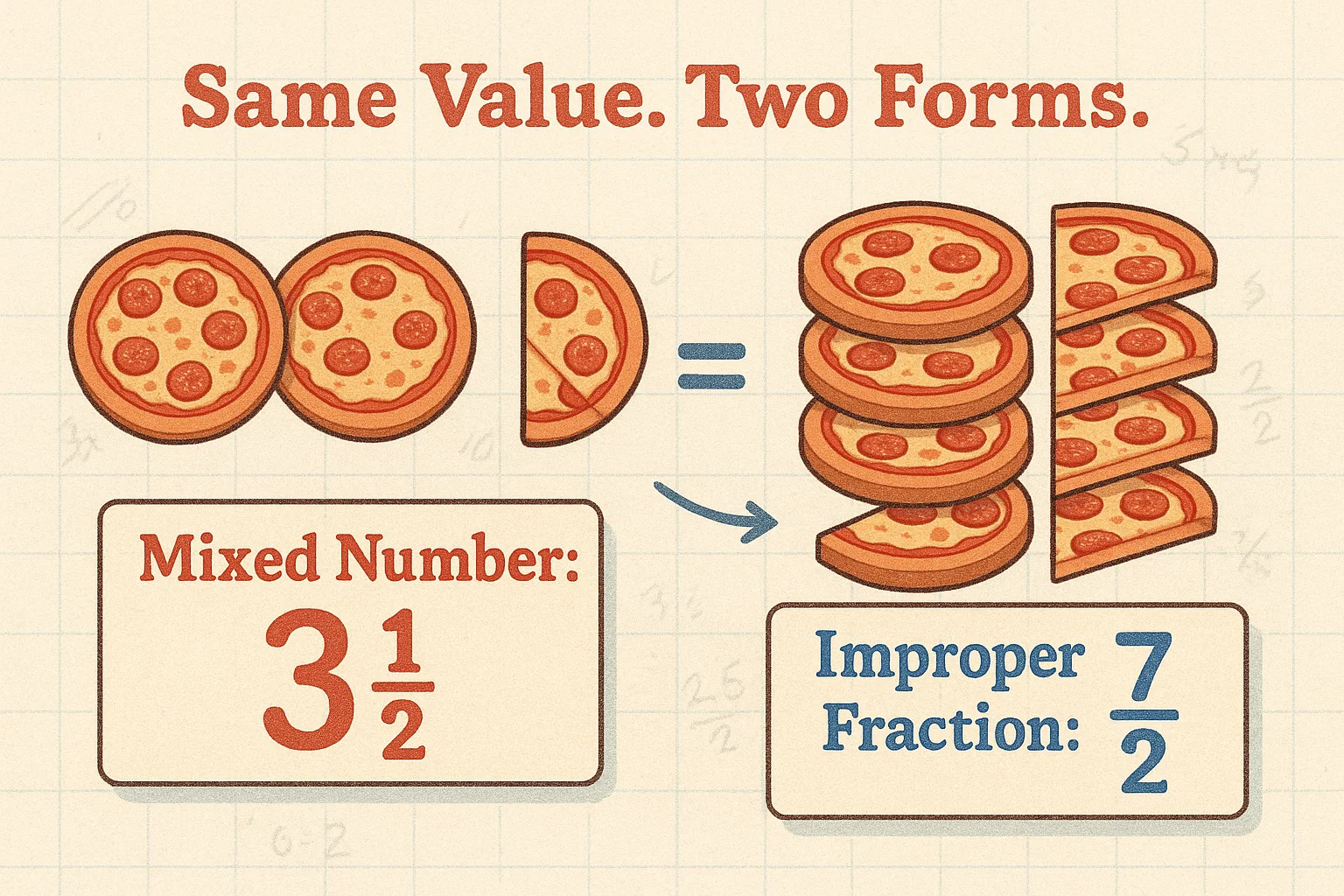
반면 가분수는 약간 더 복잡해 보이지만 같은 수학 원리를 따릅니다. 가분수는 분자(위의 숫자)가 분모(아래의 숫자)와 같거나 더 큰 분수입니다 — 예를 들어 ⁷⁄₂는 3 ½와 동등한 값이며, 다르게 표기한 것입니다.

왜 같은 값을 두 가지 형태로 표현할까요? 혼합수는 한눈에 이해하기 쉬운 반면, 가분수는 특히 대수학이나 프로그래밍에서 계산할 때 편리하기 때문입니다.

혼합수를 가분수로 변환하는 방법:

예를 들어 4 ⅗가 있다면,

1. 정수에 분모를 곱합니다: 4 × 5 = 20

2. 분자를 더합니다: 20 + 3 = 23

3. 원래 분모 위에 올립니다: ²³⁄₅

따라서 4 ⅗는 ²³⁄₅로 변환됩니다.

곱하거나 나눌 때 혼합수를 가분수로 변환하는 것은 아주 흔한 과정입니다.

가분수를 혼합수로 다시 변환하는 방법:

예를 들어 ¹¹⁄₄를 생각해 봅시다.

1. 분자를 분모로 나눕니다: 11 ÷ 4 = 2 나머지 3

2. 몫이 정수가 되고(2), 나머지가 새 분자가 됩니다(3)

3. 원래 분모를 유지합니다: 2 ¾

가분수 형태에서 시작할 때 혼합수로 간단히 만드는 방법입니다.

재미있는 사실: “아폴로 13 임무 동안 NASA 엔지니어들은 2 ⁵⁄₈와 같은 분수를 이용해 슬라이드 룰과 손 계산을 빠르게 활용하여 우주선을 우회시키고 승무원을 구했습니다.” — NASA 기록¹

분수 혼합수 계산 방법

혼합수를 더하고 빼거나 곱하고 나눌 때는 정수 부분과 분수 부분이 함께 움직여야 합니다. 핵심은 계산을 간단하고 깔끔하게 유지하며, 끝난 후 항상 약분하는 것입니다. 요리를 두 배로 만들거나 시험 문제를 풀 때 이 간단한 규칙을 따르면 빠르면서도 정확하게 계산할 수 있습니다.

더하기와 빼기

먼저 정수와 분수 부분을 분리합니다. 혼합수는 둘 다 가지고 있으므로 각각 따로 계산한 다음 다시 합칩니다.

예제를 살펴보죠:

더하기: 2 ½ + 3 ¾

1. 정수 더하기: 2 + 3 = 5

2. 분수 더하기: ½ + ¾ → 공통 분모로 변환 → ²⁄₄ + ³⁄₄ = ⁵⁄₄

3. 전체: 5 + ⁵⁄₄ → ⁵⁄₄는 1 ¼이므로 최종 결과는:
   → 6 ¼

빼기: 5 ⅚ − 2 ⅔

1. 정수 빼기: 5 - 2 = 3

2. 분수 빼기: ⁵⁄₆ − ²⁄₃ → ²⁄₃를 ⁴⁄₆로 변환 → ⁵⁄₆ − ⁴⁄₆ = ¹⁄₆

3. 최종 결과: 3 ¹⁄₆

빼기 과정에서 분수가 음수가 되면 (예: ¼ − ¾) 정수에서 빌려와야 합니다. 이 단계를 빼먹지 마세요 — 대부분의 실수가 여기서 발생합니다. 어려움이 있다면 분수 약분기로 결과를 다시 확인해 보세요.

곱하기

혼합수를 곱할 때는 항상 가분수로 변환하는 것부터 시작합니다.

예를 들어: 곱하기: 2 ⅓ × 1 ½

1. 두 혼합수를 가분수로 변환:
   2 ⅓ = ⁷⁄₃
   1 ½ = ³⁄₂

2. 분자끼리, 분모끼리 곱하기:
   ⁷⁄₃ × ³⁄₂ = ²¹⁄₆

3. 약분하기:
   ²¹⁄₆ = 3 ½

이제 계산이 완성되었습니다.

참고: “시카고 고등학교 연구에 따르면 혼합수를 가분수로 변환한 뒤 곱하기 연습을 한 학생들이 시각적으로 추측한 학생들보다 시험 점수가 27% 향상되었습니다.” — 미국 교육부 연구²

곱셈은 모든 수가 가분수 형태이므로 덧셈이나 뺄셈처럼 공통 분모를 맞출 필요가 없어 계산이 간단합니다. 곱셈이 맞는지 확신이 서지 않는다면 먼저 종이에 풀어보고 분수 계산기로 결과를 확인해 보세요.

나누기

나누기는 오해받기 쉽지만 기본적으로 곱셈의 변형일 뿐입니다.

예를 들어: 나누기: 3 ¾ ÷ 1 ½

1. 가분수로 변환:
   3 ¾ = ¹⁵⁄₄
   1 ½ = ³⁄₂

2. 나누는 수의 분수를 뒤집기:
   ³⁄₂ → ²⁄₃

3. 곱하기 수행:
   ¹⁵⁄₄ × ²⁄₃ = ³⁰⁄₁₂

4. 약분:
   ³⁰⁄₁₂ = 2 ½

끝났습니다 — 뒤집고 곱하기만 하면 됩니다.

결과가 가분수 형태(예: ²¹⁄₄)로 나와도 대수나 공식 문서에서는 그대로 사용하고, 일상에서는 혼합수(5 ¼)로 바꿔 쓰거나수학 계산기로 단계를 다시 점검할 수 있습니다.

교실이든 주방이든 이런 계산법을 알면 얼마나 숫자가 복잡해 보여도 자신 있게 다룰 수 있습니다. 결과가 가분수로 나왔다면 대수학용으로, 혼합수로 바꿔 일상 용도로 쓰거나 수학 계산기로 검증해 보세요.

한 분수가 작업 현장을 구한 이야기

혼합수는 단지 교실에만 중요한 것이 아니라 때로는 시간, 비용, 프로젝트 전반을 절약해주기도 합니다.

아이오와 주 디모인에 있는 한 건설 현장 책임자는 학교 리노베이션 작업을 거의 망칠 뻔한 한 번의 측정 실수 이야기를 공유했습니다. 설계도에는 맞춤 금속 장식 길이가 8 ⅜인치로 명시되어 있었는데, 분수 변환에 익숙하지 않은 새 견습생이 이를 8.3인치로 잘못 읽었습니다. 결과는? 검사에 떨어질 만큼 ¹⁄₁₆인치 짧은 알루미늄 패널 배치가 만들어졌습니다.

이 실수로 팀은 일주일의 재작업과 4,000달러 이상의 재료비를 잃었습니다.

“나는 직접 겪으면서 깨달았어요 — 소수점 수치는 항상 믿을 만한 게 아닙니다. 진짜 현장에서는 혼합수를 씁니다. ⅜이지 0.375가 아니고, 그 차이가 임금에도 영향을 줍니다.” — 팀 베가, Vega & Sons Build Co. 건설팀장⁴

이제 현장에서는 모든 측정값을 제작소에 보내기 전 각 공구함에 붙은 분수-소수 변환표로 두 번 확인하고, 신입 사원에게 혼합수 더하기 빼기를 공통 분모를 이용해 빠르게 가르칩니다.

혼합수는 그저 학문적 지식이 아닙니다. 설계도, 요리법, 청구서, 스포츠 통계, 심지어 도구 교정에도 등장합니다. 이 계산법에 익숙해지는 것은 시험을 위한 것이 아니라, 줄자 들고 실생활에서 자신 있게 움직이기 위한 것입니다.

1. NASA. “Apollo 13 Timeline.”

2. 미국 교육부. “고등학교 수학 연구.”

3. Napa Valley College 제빵 및 요리 프로그램, 사례 인터뷰, 2023년 3월

4. 팀 베가 인터뷰, 2022년 6월. 아이오와 공공안전부 건축 기준 및 검사